
Jump, split or make to the next 10: strategies to teach maths have changed since parents were at school
Comment 17 Dec 2020 8 minute readResearch shows parents have a significant influence on their children's learning, but some lack the confidence to provide at home support. To help parents engage with their children's maths learning, The Conversation asked ACER Senior Research Fellow Cath Pearn to explain three addition and subtraction strategies now taught in primary school.
I’m sure most people can remember trying to master a certain maths rule or procedure in primary or secondary school.
My elderly mother has a story about a time her father was helping her with arithmetic homework. She remembers getting upset because her father did not do it “the school way”. I suspect her father was able to do the calculation mentally rather than the school way, which was to use the vertical algorithm.
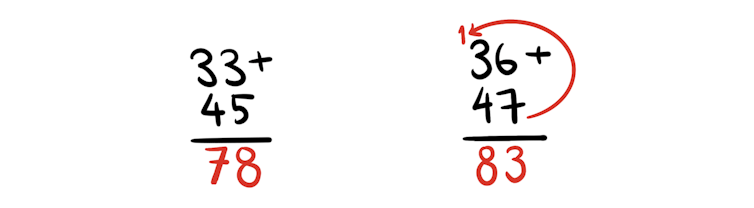
Students are expected to add the numbers in the ones (right) column first, before adding the numbers in the tens (left) column. The task becomes more difficult when the total of the ones column is more than 10 — as you then have to “trade” ten ones for one ten.
Students who give the answer as 713 rather than the correct answer of 83 may well have started with the tens column first. Or they may have written 13 in the ones column rather than trading ten ones for one ten.
The formal school algorithms are still used for larger numbers and decimals but we encourage students to use whichever strategy they prefer for two-digit addition.
The trouble with teaching rules is many students then struggle to remember when to apply the rule because they don’t understand how or why the rule works.
The Australian Curriculum: Mathematics states that by the end of year 2, students will “perform simple addition and subtraction calculations using a range of strategies”. By the end of year 4, they will “identify and explain strategies for finding unknown quantities in number sentences”.
We want children to remember how to do these equations in their head, rather than relying on writing down the process. Here are three strategies schools use to teach children how to add and subtract two-digit numbers.
1. Split strategy
This is sometimes called the decomposition, partitioning or partial-sums strategy.
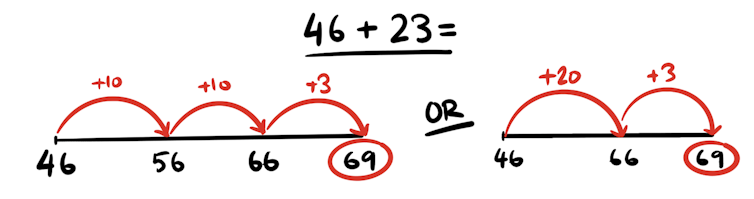
You can add or subtract the tens separately to the ones (or units). For example, using the split strategy to add 46 + 23, you would:
-
split each number (decompose) into tens and ones: 46 + 23 = 40 + 6 + 20 + 3
-
rearrange the tens and ones: 40 + 20 + 6 + 3
-
add the tens and then the ones 60 + 9 = 69
Using the split strategy for addition such as 37 + 65 would be similar, but there would be an extra step:
-
split or decompose the numbers into tens and ones: 30 + 7 + 60 + 5
-
rearrange the tens and ones: 30 + 60 + 7 + 5
-
add the tens and then the ones: 90 + 12
-
split 12 (10 + 2) to give: 90 + 10 + 2 = 100 + 2 = 102
Many students find the split strategy more difficult for subtraction than addition. This is because there are more steps if performing this strategy mentally.
For a subtraction such as 69 – 46, you would:
-
split or decompose each number into tens and ones: 60 + 9 – (40 + 6)
-
remove bracket: 60 + 9 – 40 – 6
-
rearrange tens and ones: (60 – 40) + (9 – 6)
-
subtract the tens, then the ones: 20 + 3 = 23
Students often make mistakes in the third step. Successful students may say: “I take 40 from 60, then 6 from 9”. Unsuccessful students will say “I take 40 from 60 then add 6 and 9”.
Students who use this strategy successfully are showing they understand place value (the value of each digit in a number) and their knowledge of maths rules needed for algebra.
2. Jump strategy
This is sometimes called the sequencing or cumulative sums strategy. The actual steps taken depend on the confidence and ability of the students.
Some students add increments of tens or ones, while others add or subtract multiples of tens then ones.
For example, adding 46 + 23 using the jump strategy might look like this:
-
add two lots of ten to 46: 46 + 10 = 56, then 56 + 10 = 66
-
add the remaining 3: 66 + 3 = 69
or
-
add 20 to 46 which becomes 66
-
add the remaining 3: 66 + 3 = 69
The two versions of this strategy can be shown using an empty number line. Using a blank or empty number line allows student to record their thinking and for teachers to analyse their thinking and determine the strategy they have attempted to use.
Subtracting 69 – 46 with the jump strategy could be done by:
-
subtracting four lots of ten (40) from 69: 69 – 10 = 59; 59 – 10 = 49; 49 – 10 = 39; 39 – 10 = 29
-
then finally subtracting the remaining 6: 29 – 6 = 23
or
-
subtract 40: 69 – 40 = 29
-
then subtract 6: 29 – 6 = 23
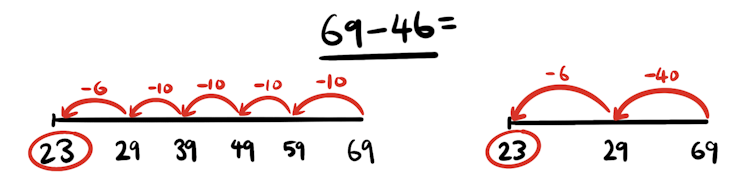
3. ‘Make to the next ten’ strategy
This is sometimes called the compensation or shortcut strategy. It involves adjusting one number to make the task easier to solve.
The “make to the next ten” strategy builds on the “friends of ten” strategy.
Many students in the first years of primary school create all the combinations of two single digit numbers that give a total of ten.
9 + 1, 8 + 2, 7 + 3, 6 + 4, 5 + 5 …
These are sometimes called the rainbow facts as the children create rainbows as they connect two numbers together. For instance, 9 may be on one end of a rainbow colour and 1 on the other.
By combining the numbers in this way teachers hope students will realise the answer for 9 + 1 is the same as 1 + 9.
In the “make to the next ten” strategy, you add or subtract a number larger than the number given (such as the next multiple of ten) and then readjust the number by subtracting what was added or adding what was subtracted.
In the diagrams the relationships are indicated by the use of arrows.
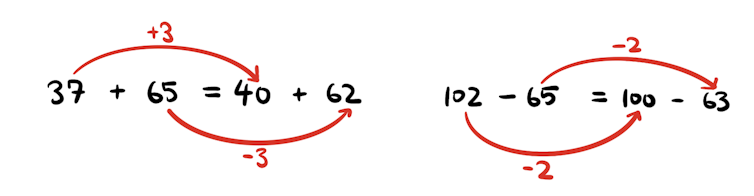
So, to add 37 + 65, you would
-
add 3 to 37 to give 40.
-
subtract 3 from 65 to get 62
-
this becomes: 40 + 62 = 102.
If subtracting 102 – 65, you would:
-
subtract 2 from 102 to make 100
-
subtract 2 from 65 to maintain the balance
-
this becomes 100 – 63 = 37.
Many students using this strategy incorrectly add 2 to 65 instead of subtracting 2.
Why these strategies?
Students would have been using all these strategies, or some forms of them, in their head for generations. But for many years, the expectation was that students use the formal written algorithm rather than their own mental strategies.
The introduction of the empty or blank number line allowed students to record their mental strategies, which allowed teachers and parents to see them. Naming these strategies has allowed teachers and students to discuss possible strategies using a common vocabulary.
Rather than teach rules and procedures, we now need to encourage students to explain their strategies using both concrete materials and diagrams to demonstrate their knowledge of addition and subtraction.![]() ■
■
Further information:
This article by Cath Pearn, Senior Research Fellow, Australian Council for Educational Research, is republished from The Conversation under a Creative Commons license. Read the original article.